Difference between revisions of "Interpretação quântica de três polarizadores"
Jump to navigation
Jump to search
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | [[File:Data Analise Polaroid.png|240|thumb| Se realizarmos a experiência rodando pelo menos 90º, fica claro pelos resultados obtidos que podemos esperar uma probabilidade de um fótão passar por um polarizador proporcional a uma função sinusoidal, já que no estado ortogonal ao polarizador nenhum fotão pode passar. Pelo contrário, em um estado alinhado, a probabilidade de passagem é de 100%.]] | |
| − | Vamos descrever o estado de polarização | + | Se realizarmos a experiência da [[Polarização_da_Luz|Polarização]] fazendo um varrimento de 180°, observaremos que a probabilidade de passagem/transmissão dos fotões é proporcional a uma função sinusoidal, como um <math>sin^2(\theta)</math>. Contudo, o seno precisa ser elevado ao quadrado, pois nenhuma probabilidade pode ser negativa. Note-se que <math>sin^2(\theta)</math> ainda é uma função sinusoidal. |
| + | |||
| + | Vamos descrever o estado de polarização do fotão como um vetor bidimensional, em que a luz polarizada verticalmente corresponde a um vetor apontando para cima (0, 1), enquanto a luz polarizada horizontalmente, ortogonal ao polarizador, corresponde a (1, 0). Usamos a notação de Dirac para representar esses vetores, ''|V>'' e ''|H>'', respectivamente. Um vetor arbitrário pode ser escrito então como \(|α〉=cos(α) |V〉+ sin(α) |H〉 \). | ||
A mecânica quântica explica como calcular: | A mecânica quântica explica como calcular: | ||
| − | + | # a probabilidade de transmissão desses estados através de um polarizador; | |
| − | + | # o estado na saída do polarizador. Quando o estado \(|V>\) passa pelo segundo polarizador, orientado, por exemplo, a 45°, temos que a probabilidade de transmissão é dada por: | |
| − | + | ||
| + | <math> | ||
| + | Prob=|〈V|P_{(45°)} |V〉|^2=1/2 | ||
| + | </math> | ||
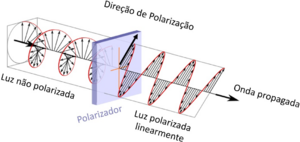
| + | [[File:Light Polarization Diagram.png|240|thumb| Interpretação clássica da polarização da luz. Esta interpretação só é possível para um número imenso de fotões; para um único ou poucos fotões, precisamos assumir um estado quantizado associado a cada fotão.]] | ||
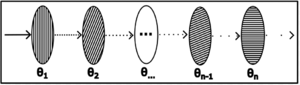
| + | [[File:Multi Polaroid.png|240|thumb| No caso de vários polarizadores com um pequeno ângulo incremental até ao final em 90º, pode-se mostrar que a probabilidade de o fotão passar pela cascata de polarizadores torna-se progressivamente maior, chegando a 100% para um número infinito de polarizadores!]] | ||
| + | <!-- [[File:Experimental SetUp Polaroid.png|240|thumb| Configuração do experimento paradoxo dos três polarizadores.]]--> | ||
| + | |||
| + | Assim, o comportamento do fotão através de um polarizador pode ser interpretado como: | ||
| + | |||
| + | #'''Estado Inicial de Polarização:''' Um fotão que se aproxima de um polarizador tem um estado de polarização específico, que pode ser representado como uma superposição dos dois estados base definidos pelo eixo do polarizador: (i) alinhado paralelamente a este ou no estado vertical e (ii) ortogonal ou no estado horizontal. | ||
| + | #'''Interação com o Polarizador:''' Ao encontrar o polarizador, o estado de polarização do fotão é "medido" em relação ao eixo do polarizador. Esse processo projeta a polarização do fotão em um dos dois eixos ortogonais entre si: (i) Paralelo ao eixo do polarizador (transmitido) ou (ii) Perpendicular ao eixo do polarizador (absorvido ou bloqueado). A probabilidade de transmissão do fotão é dada por \(P_{transmitido}=cos^{2}(\theta)\), onde <i>θ</i> é o "ângulo" que fornece a probabilidade entre os dois estados, o que, na teoria clássica, se resume ao ângulo com o eixo do polarizador. | ||
| + | #'''Estado Pós-Polarizador:''' Se o fotão passa, de acordo com a dada probabilidade, o seu estado de polarização agora está definitivamente alinhado com o eixo do polarizador pelo qual acabou de passar (ele não mantém mais o seu estado de polarização original, sendo esta uma distinção fundamental para a teoria clássica). | ||
| + | |||
| + | Agora, se tivermos uma cadeia de polarizadores, ou seja, se vários polarizadores forem colocados em sequência, com cada polarizador sucessivo girado por um pequeno ângulo <i>Δθ</i>, a probabilidade total de um fotão passar por todos os <i>N</i> polarizadores é: | ||
<math> | <math> | ||
| − | + | P_{total}=\prod_{i=1}^{N−1} cos^{2}(Δθ) | |
</math> | </math> | ||
| + | onde \(Δθ=\frac{90º}{(N−1)}\) | ||
| + | |||
| + | Isso simplifica para: | ||
| + | |||
| + | <math> | ||
| + | P_{total}=(cos^{2}(Δθ))^{N−1} | ||
| + | </math> | ||
| + | '''Exemplo:''' | ||
| − | + | Suponha que sejam usados ''N=10'' polarizadores para ir de ''θ=0º'' a ''θ=90º''. Então, \( Δθ=90º/9=10º\). | |
| + | *''Probabilidade de passagem em cada etapa:'' \( P_i=cos^{2}(10º)≈0,97 \). | ||
| + | *''Probabilidade total:'' \(P_{total}=(0.9698)^9≈0.75\) | ||
| − | + | Este resultado mostra que uma rotação gradual por sucessivos polarizadores aumenta a probabilidade de transmissão em comparação ao uso de apenas dois polarizadores orientados a ''0º'' e ''90º'', onde nenhum fotão passaria nesta situação, já que \(cos^{2}(90º)=0\). | |
| − | + | '''Pontos-chave para clarificação:''' | |
| + | * O fotão não ''mantém'' seu estado de polarização original se atravessar o polarizador; em vez disso, adquire um novo estado alinhado com o eixo do polarizador. | ||
| + | * O resultado é probabilístico: um fotão pode ou não passar por um polarizador, baseado na projeção de seu estado inicial de polarização no eixo desse polarizador. | ||
| + | * Esse fenômeno realça os princípios da mecânica quântica de colapso de estado e medição, distintos da explicação clássica por ondas eletromagnéticas. | ||
| − | [[ | + | =Ligações= |
| + | *[[Light Polarization | Versão em Inglês (English Version)]] | ||
| + | *[[Deus joga dados! | Deus joga dados - o Jogo]] | ||
Latest revision as of 09:48, 12 April 2025
Se realizarmos a experiência rodando pelo menos 90º, fica claro pelos resultados obtidos que podemos esperar uma probabilidade de um fótão passar por um polarizador proporcional a uma função sinusoidal, já que no estado ortogonal ao polarizador nenhum fotão pode passar. Pelo contrário, em um estado alinhado, a probabilidade de passagem é de 100%.
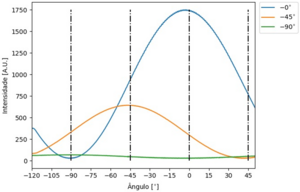
Se realizarmos a experiência da Polarização fazendo um varrimento de 180°, observaremos que a probabilidade de passagem/transmissão dos fotões é proporcional a uma função sinusoidal, como um [math]sin^2(\theta)[/math]. Contudo, o seno precisa ser elevado ao quadrado, pois nenhuma probabilidade pode ser negativa. Note-se que [math]sin^2(\theta)[/math] ainda é uma função sinusoidal.
Vamos descrever o estado de polarização do fotão como um vetor bidimensional, em que a luz polarizada verticalmente corresponde a um vetor apontando para cima (0, 1), enquanto a luz polarizada horizontalmente, ortogonal ao polarizador, corresponde a (1, 0). Usamos a notação de Dirac para representar esses vetores, |V> e |H>, respectivamente. Um vetor arbitrário pode ser escrito então como \(|α〉=cos(α) |V〉+ sin(α) |H〉 \).
A mecânica quântica explica como calcular:
- a probabilidade de transmissão desses estados através de um polarizador;
- o estado na saída do polarizador. Quando o estado \(|V>\) passa pelo segundo polarizador, orientado, por exemplo, a 45°, temos que a probabilidade de transmissão é dada por:
[math] Prob=|〈V|P_{(45°)} |V〉|^2=1/2 [/math]
Assim, o comportamento do fotão através de um polarizador pode ser interpretado como:
- Estado Inicial de Polarização: Um fotão que se aproxima de um polarizador tem um estado de polarização específico, que pode ser representado como uma superposição dos dois estados base definidos pelo eixo do polarizador: (i) alinhado paralelamente a este ou no estado vertical e (ii) ortogonal ou no estado horizontal.
- Interação com o Polarizador: Ao encontrar o polarizador, o estado de polarização do fotão é "medido" em relação ao eixo do polarizador. Esse processo projeta a polarização do fotão em um dos dois eixos ortogonais entre si: (i) Paralelo ao eixo do polarizador (transmitido) ou (ii) Perpendicular ao eixo do polarizador (absorvido ou bloqueado). A probabilidade de transmissão do fotão é dada por \(P_{transmitido}=cos^{2}(\theta)\), onde θ é o "ângulo" que fornece a probabilidade entre os dois estados, o que, na teoria clássica, se resume ao ângulo com o eixo do polarizador.
- Estado Pós-Polarizador: Se o fotão passa, de acordo com a dada probabilidade, o seu estado de polarização agora está definitivamente alinhado com o eixo do polarizador pelo qual acabou de passar (ele não mantém mais o seu estado de polarização original, sendo esta uma distinção fundamental para a teoria clássica).
Agora, se tivermos uma cadeia de polarizadores, ou seja, se vários polarizadores forem colocados em sequência, com cada polarizador sucessivo girado por um pequeno ângulo Δθ, a probabilidade total de um fotão passar por todos os N polarizadores é:
[math] P_{total}=\prod_{i=1}^{N−1} cos^{2}(Δθ) [/math]
onde \(Δθ=\frac{90º}{(N−1)}\)
Isso simplifica para:
[math] P_{total}=(cos^{2}(Δθ))^{N−1} [/math]
Exemplo:
Suponha que sejam usados N=10 polarizadores para ir de θ=0º a θ=90º. Então, \( Δθ=90º/9=10º\).
- Probabilidade de passagem em cada etapa: \( P_i=cos^{2}(10º)≈0,97 \).
- Probabilidade total: \(P_{total}=(0.9698)^9≈0.75\)
Este resultado mostra que uma rotação gradual por sucessivos polarizadores aumenta a probabilidade de transmissão em comparação ao uso de apenas dois polarizadores orientados a 0º e 90º, onde nenhum fotão passaria nesta situação, já que \(cos^{2}(90º)=0\).
Pontos-chave para clarificação:
- O fotão não mantém seu estado de polarização original se atravessar o polarizador; em vez disso, adquire um novo estado alinhado com o eixo do polarizador.
- O resultado é probabilístico: um fotão pode ou não passar por um polarizador, baseado na projeção de seu estado inicial de polarização no eixo desse polarizador.
- Esse fenômeno realça os princípios da mecânica quântica de colapso de estado e medição, distintos da explicação clássica por ondas eletromagnéticas.
