Determination of Planck's Constant

Description of the Experiment

In this experiment is possible study the photoelectric effect and calculate Planck's constant. Using 5 colored leds and a photoelectric cell.

Experimental Apparatus

Figure 1: Led's spectrum.

The photoelectric cell is from the apparatus PASCO AP-9368. It works like a capacitor where an electric conductor emits photoelectrons. The potential of the photocell will increase with the emission of photoelectrons. And the stop potential will depend on the wavelength of the incident light, photoelectric effect.

The photocell is connected to ground to discharge, after each use.

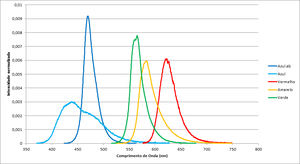
The leds have different spectrum and intensities so the time to reach the stop potencial may vary.

Table 1 – Led's spectrum peaks

Color	Frequency (THz)	Wavelegth (nm)	Espectros dos leds
Blue.ab	638.7	469.70	File:Espectro Azul.ab.txt
Blue	684.6	438.20	File:Espectro Azul.txt
Red	482.2	622.21	File:Espectro Vermelho.txt
Yellow	514.4	583.16	File:Example.txt
Green	530.8	565.22	File:Espectro Verde.txt

Protocol

The number of photoelectrons emited will increase with the intensity of light. (corpuscular behavior of light)

1. Choose a led to light up on the photocell
2. Measure the stopping potential. Take note the time necessary to reach the maximum potential.
3. Repit step 2 for diferent intensities.

Exemple of a table

Color #1 __________(name)	Intensity (%)	Stop Potential (V)	Time (s)
	100
	80
	60
	40
	20

Figure 2: Potential vs. Peaks Frequency of the spectrum

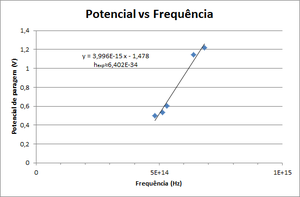
The photoelectron's kinetic energy depend only on the frequency of light. If the frequency of light increase the energy will increase.

1. Obtain the stop potentials for different color leds.
2. Draw a graphic of Stop Potential vs Frequency. Fit it $V = \frac{h \times \nu}{e} - \frac{W_0}{e}$ to and obtain Planck's constant.

Exemple of a table

Color (name)	Frequency (Hz)	Stop Potencial (V)