Difference between revisions of "Plano Inclinado"
| Line 37: | Line 37: | ||
Um detector ultra-sónico colhe então amostras da posição em função do tempo decorrido, permitindo traçar a trajectória do veículo durante a queda e no seu amortecimento final. | Um detector ultra-sónico colhe então amostras da posição em função do tempo decorrido, permitindo traçar a trajectória do veículo durante a queda e no seu amortecimento final. | ||
| − | |||
| − | |||
| − | |||
==Protocolo== | ==Protocolo== | ||
Com base nos dados pré-seleccionados na experiência obtenha um gráfico da posição em função do tempo decorrido. Com base nestes dados determine ainda os gráficos da velocidade e da aceleração. Compare o valor obtido da aceleração com a gravidade. | Com base nos dados pré-seleccionados na experiência obtenha um gráfico da posição em função do tempo decorrido. Com base nestes dados determine ainda os gráficos da velocidade e da aceleração. Compare o valor obtido da aceleração com a gravidade. | ||
| + | |||
| + | ===Determinação da velocidade em função da distância percorrida=== | ||
| + | Com base nos dados anteriores determine a velocidade em função da distância percorrida, eliminando o tempo nos gráficos anteriores, ou seja, traçando a curva desenhada pelos pares velocidade, distância para cada tempo disponível. | ||
| + | |||
| + | ===Determinação da constante de restituição da mola=== | ||
| + | |||
| + | Em função das várias parábolas obtidas no amortecimento do veículo, determine a perda relativa de energia em cada embate com a mola e determine a constante de restituição da mola. | ||
==Protocolo avançado== | ==Protocolo avançado== | ||
| − | + | Como pode ser inferido rapidamente, o ajuste do modelo parabólico ao movimento produz um desvio só possivel de entender com a inclusão dum termo de fricção. Com efeito o carrinho dispõe duma pala frontal destinada a induzir um certo atrito aerodinâmico. Adaptando as equações de modo a incluir um termo de atrito de rolamento (linear com a velocidade) e aerodinâmico (Cx, dependencia quadrática com a velocidade), pode-se determinar finalmente um valor mais preciso para a aceleração do veículo. | |
| − | |||
Normalmente o ''Cx'' só influência significativamente o movimento a partir dos 25 km/h. | Normalmente o ''Cx'' só influência significativamente o movimento a partir dos 25 km/h. | ||
| − | === | + | O ajuste duma função de atrito para a aceleração na forma ''a = b + c*v + d*v<sup>2</sup>'' permite extrair a aceleração local da gravidade ao serem utilizadas várias séries de dados para ângulos variados. |
| − | + | ||
| + | ===Modelo multivariado=== | ||
| + | A análise multivariada utilizada serve para construir um modelo de ajuste numérido para vários ângulos às várias características do movimento obtido. A variação do ângulo permite com efeito distinguir o efeito da gravidade da força de atrito de rolamento já que este é considerado independente do ângulo. Dete modo, ao fazer um ajuste do tipo a = b + c*v + d*v2 o parâmetro b que detém implicitamente a gravidade e o atrito de rolamento (relacionado com a mecânica do veículo) pode ser resolvido separando-o em b=g*sin(θ) + batrito . Os restantes parâmetros resultam dum modelo da dependência do atrito com a velocidade que para valores elevados desta (tipicamente superior a 7-10 ms-1) tem uma forte dependência quadrática na velocidade – atrito aerodinâmico – mas que no nosso caso também temos de considerar a dependência de atrito mecânico (batrito+c*v) uma vez que o carro parte do repouso. | ||
| + | Ao realizar esta análise multivariada estamos a considerar uma associação independente entre os parâmetros, condição necessária para esses parâmetros fazerem parte de um modelo numérico que se provará correto pelo desfecho do ajuste. Para o efeito usaremos o solver do MSExcel ajustando iterativamente as várias co-variáveis. | ||
===Determinação da constante de restituição da mola=== | ===Determinação da constante de restituição da mola=== | ||
| − | + | Uma análise breve permite concluir que a constante de restituição da mola para os vários embates vem ferida dum erro apreciável, tanto maior quanto o percurso percorrido, uma vez que o trabalho realizado pela força de atrito prejudica o cálculo da energia mecânica em cada troço do movimento. No entanto, calculando o trabalho efetuado pela força de atrito com base na equação da força de atrito determinada pelo processo anteriormente descrito, permite inferir corretamente a energia mecânica antes e depois de cda embate, permitindo calcular corretamente a constante de restituição da mola. | |
| + | |||
==Ligações== | ==Ligações== | ||
*[[Inclined plane | This page in English]] | *[[Inclined plane | This page in English]] | ||
Revision as of 16:13, 20 August 2020
Contents
Plano inclinado
Descrição da experiência
O plano inclinado é uma das seis máquinas simples clássicas. Os planos inclinados são geralmente utilizados para mover cargas pesadas sobre obstáculos verticais tais como rampas para mover carga.
Mover um objeto para cima em um plano inclinado requer menos força do que levantá-lo na vertical, como se desmultiplicassemos a gravidade! Esta vantagem mecânica pelo qual a força é reduzida é igual à razão entre o comprimento da superfície inclinada e a altura em que se estende a rampa.
Nas experiências laboratoriais que recriam esta máquina, na situação em que não é usada uma calha de ar de modo a quase eliminar o atrito de rolamento, tem de ser usado um ângulo significativo de forma à aceleração gravítica ser muito superior ao atrito, eliminando a vantagem da experiência poder ser realizada num tempo grande, percetível aos sentidos humanos.
Contudo o atrito faz parte integrante da mecânica do problema e esta experiência permite determinar a função de atrito através duma análise multi-variada ajustando uma função que dependa da inclinação da calha. A experiência para o efeito, permite alterar o ângulo de descida e, através deste, separar as forças de atrito da gravítica, obtendo-se um valor muito próximo de 9,8 ms-2.
Ligações
- Video: rtsp://elabmc.ist.utl.pt/plinc.sdp
- Laboratory: Básico
- Control room: Plano inclinado
- Level: *
Propositadamente nesta experiência é usado um carro equipado com um pára-vento frontal de modo a exarcebar o efeito do atrito e demonstrar que a sua equação pode ser determinada pela anáside multivariada de vários percursos para ângulos váriados.
Aparato experimental
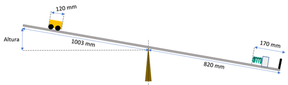
O plano inclinado desta experiência recria essa "desmultiplicação da gravidade". Consiste num veículo que se desloca numa calha com um ângulo regulavel e que bascula no seu ponto médio. A altura da calha é medida a 1003 mm do eixo da experiência.
Inicialmente a calha bascula para uma posição com um ângulo negativo de modo a recolher e a parquear o carro na origem, a cerca de 1,3m da mola que irá absorver a energia do seu movimento. Este é imobilizado através dum eletroímã e posteriormente a calha é elevada até à altura pré-seleccionada. Quando atinge esse ponto, o electroímane liberta o carrinho e este desloca-se livremente sobre a calha até embater na mola. Um detector ultra-sónico colhe então amostras da posição em função do tempo decorrido, permitindo traçar a trajectória do veículo durante a queda e no seu amortecimento final.
Protocolo
Com base nos dados pré-seleccionados na experiência obtenha um gráfico da posição em função do tempo decorrido. Com base nestes dados determine ainda os gráficos da velocidade e da aceleração. Compare o valor obtido da aceleração com a gravidade.
Determinação da velocidade em função da distância percorrida
Com base nos dados anteriores determine a velocidade em função da distância percorrida, eliminando o tempo nos gráficos anteriores, ou seja, traçando a curva desenhada pelos pares velocidade, distância para cada tempo disponível.
Determinação da constante de restituição da mola
Em função das várias parábolas obtidas no amortecimento do veículo, determine a perda relativa de energia em cada embate com a mola e determine a constante de restituição da mola.
Protocolo avançado
Como pode ser inferido rapidamente, o ajuste do modelo parabólico ao movimento produz um desvio só possivel de entender com a inclusão dum termo de fricção. Com efeito o carrinho dispõe duma pala frontal destinada a induzir um certo atrito aerodinâmico. Adaptando as equações de modo a incluir um termo de atrito de rolamento (linear com a velocidade) e aerodinâmico (Cx, dependencia quadrática com a velocidade), pode-se determinar finalmente um valor mais preciso para a aceleração do veículo. Normalmente o Cx só influência significativamente o movimento a partir dos 25 km/h.
O ajuste duma função de atrito para a aceleração na forma a = b + c*v + d*v2 permite extrair a aceleração local da gravidade ao serem utilizadas várias séries de dados para ângulos variados.
Modelo multivariado
A análise multivariada utilizada serve para construir um modelo de ajuste numérido para vários ângulos às várias características do movimento obtido. A variação do ângulo permite com efeito distinguir o efeito da gravidade da força de atrito de rolamento já que este é considerado independente do ângulo. Dete modo, ao fazer um ajuste do tipo a = b + c*v + d*v2 o parâmetro b que detém implicitamente a gravidade e o atrito de rolamento (relacionado com a mecânica do veículo) pode ser resolvido separando-o em b=g*sin(θ) + batrito . Os restantes parâmetros resultam dum modelo da dependência do atrito com a velocidade que para valores elevados desta (tipicamente superior a 7-10 ms-1) tem uma forte dependência quadrática na velocidade – atrito aerodinâmico – mas que no nosso caso também temos de considerar a dependência de atrito mecânico (batrito+c*v) uma vez que o carro parte do repouso. Ao realizar esta análise multivariada estamos a considerar uma associação independente entre os parâmetros, condição necessária para esses parâmetros fazerem parte de um modelo numérico que se provará correto pelo desfecho do ajuste. Para o efeito usaremos o solver do MSExcel ajustando iterativamente as várias co-variáveis.
Determinação da constante de restituição da mola
Uma análise breve permite concluir que a constante de restituição da mola para os vários embates vem ferida dum erro apreciável, tanto maior quanto o percurso percorrido, uma vez que o trabalho realizado pela força de atrito prejudica o cálculo da energia mecânica em cada troço do movimento. No entanto, calculando o trabalho efetuado pela força de atrito com base na equação da força de atrito determinada pelo processo anteriormente descrito, permite inferir corretamente a energia mecânica antes e depois de cda embate, permitindo calcular corretamente a constante de restituição da mola.