Difference between revisions of "Determinação da Constante Dieléctrica num Condensador Cilíndrico"
| Line 21: | Line 21: | ||
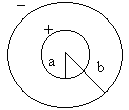
[[File:condensador-seccao.png|thumb|Figura 2: Secção do condensador, onde a=12mm e b=14mm]] | [[File:condensador-seccao.png|thumb|Figura 2: Secção do condensador, onde a=12mm e b=14mm]] | ||
| − | O condensador cilíndrico é formado por um tubo de cobre de 12mm de diâmetro exterior e 200mm de comprimento, cuja periferia inicial está | + | O condensador cilíndrico é formado por um tubo de cobre de 12mm de diâmetro exterior e 200mm de comprimento (armadura interior), cuja periferia inicial está recoberta com um dielétrico de Poliestireno até um certo ponto. Este é inserido num outro tubo de cobre com 14mm interiores (armadura exterior) que se desloca sobre o primeiro, constituindo desta forma as armaduras dum consensador variável. Deste modo a área util do condensador corresponde na prática às zonas de sobreposição em que o segundo tubo circunda o primeiro. |
| + | Note-se que, por constrangimentos de montagem, há 26mm de condensador "mínimo". Ou seja, x=0 corresponde a um condensador cilíndrico com 26mm de comprimento. | ||
| + | <!-- | ||
Esta configuração é equivalente a dois condensadores variáveis cuja capacidade total corresponde a um paralelo entre este sistema e um condensador fixo (capacidade inicial). | Esta configuração é equivalente a dois condensadores variáveis cuja capacidade total corresponde a um paralelo entre este sistema e um condensador fixo (capacidade inicial). | ||
| + | |||
A experiência devolve ao utilizador o período da frequência de oscilação do circuito RC formado com esta capacidade e uma resistência de 1,8 \( M \Omega \). | A experiência devolve ao utilizador o período da frequência de oscilação do circuito RC formado com esta capacidade e uma resistência de 1,8 \( M \Omega \). | ||
O valor do período do circuito oscilante é dado por \( T= \frac{RC}{1,44} \). | O valor do período do circuito oscilante é dado por \( T= \frac{RC}{1,44} \). | ||
| + | --> | ||
=Protocolo= | =Protocolo= | ||
| + | |||
==Determinação da constante dielétrica relativa== | ==Determinação da constante dielétrica relativa== | ||
| − | Recolhe-se dois conjuntos de pontos experimentais, o primeiro cobrindo uma zona com dielétrico e outra com ar. Devem ser escolhidos dois limites de varrimento adequado de modo a conseguir determinar os declives das | + | Recolhe-se dois conjuntos de pontos experimentais, o primeiro cobrindo uma zona com dielétrico e outra com ar. Devem ser escolhidos dois limites de varrimento adequado de modo a conseguir determinar os declives das rectas com alguma precisão (tomando atenção ao número de pontos escolhido). |
| − | O declive da primeira reta (comprimentos menores) permite estabelecer a relação | + | O declive da primeira reta (comprimentos menores) permite estabelecer a relação entre o comprimento e a carga de um condensador cilíindrico cujo dieléctrico é Poliestireno, a segunda recta é equivalente para um condensador de ar. |
| − | A razão dos dois declives será | + | A razão dos dois declives será igual á constante dielétrica relativa do PVC. |
=Protocolo Avançado= | =Protocolo Avançado= | ||
| + | |||
==Determinação da constante dielétrica do ar== | ==Determinação da constante dielétrica do ar== | ||
Considerando a lei de Gauss, consegue-se determinar a capacidade do condensador cilindrico cuja expressão é dada por | Considerando a lei de Gauss, consegue-se determinar a capacidade do condensador cilindrico cuja expressão é dada por | ||
\[ | \[ | ||
| − | C = 2 | + | C = \frac{ 2 \pi \epsilon _0 }{ ln(\frac{b}{a}) } L |
\] | \] | ||
| − | Efetuando uma regressão linear sobre a secção sem dielétrico (ou seja, o dielétrico é o ar) consegue-se determinar o valor da capacidade com elevada confiança. Com base neste valor, invertendo a fórmula, determina-se o valor da permitividade do ar (próximo do vazio, ou seja, \( \epsilon _0 \)). | + | Efetuando uma regressão linear sobre a secção sem dielétrico (ou seja, onde o dielétrico é o ar) consegue-se determinar o valor da capacidade com elevada confiança. Com base neste valor, invertendo a fórmula, determina-se o valor da permitividade do ar (próximo do vazio, ou seja, \( \epsilon _0 \)). |
=Ligações= | =Ligações= | ||
*[[Dielectric effect in a Cilindric Capacitor | Versão em Inglês (English Version)]] | *[[Dielectric effect in a Cilindric Capacitor | Versão em Inglês (English Version)]] | ||
| + | *[http://pt.wikipedia.org/wiki/Poliestireno | Página da Wikipédia sobre o Poliestireno | ||
Revision as of 01:09, 21 March 2013
Contents
Descrição da Experiência
Esta experiência destina-se a determinar a capacidade de um condensador cilíndrico coaxial variável. Este dispõe de duas secções, uma inicial com um dieléctrico diferente do ar, de PVC, e um segundo troço de ar, permitindo determinar a constante dielétrica relativa do PVC.
Ligações
- Video: rtsp://elabmc.ist.utl.pt/condensador.sdp
- Laboratório: Avançado em e-lab.ist.eu[1]
- Sala de controlo: Condensador Cilíndrico
- Nivel: ****
Aparato Experimental
O condensador cilíndrico é formado por um tubo de cobre de 12mm de diâmetro exterior e 200mm de comprimento (armadura interior), cuja periferia inicial está recoberta com um dielétrico de Poliestireno até um certo ponto. Este é inserido num outro tubo de cobre com 14mm interiores (armadura exterior) que se desloca sobre o primeiro, constituindo desta forma as armaduras dum consensador variável. Deste modo a área util do condensador corresponde na prática às zonas de sobreposição em que o segundo tubo circunda o primeiro.
Note-se que, por constrangimentos de montagem, há 26mm de condensador "mínimo". Ou seja, x=0 corresponde a um condensador cilíndrico com 26mm de comprimento.
Protocolo
Determinação da constante dielétrica relativa
Recolhe-se dois conjuntos de pontos experimentais, o primeiro cobrindo uma zona com dielétrico e outra com ar. Devem ser escolhidos dois limites de varrimento adequado de modo a conseguir determinar os declives das rectas com alguma precisão (tomando atenção ao número de pontos escolhido). O declive da primeira reta (comprimentos menores) permite estabelecer a relação entre o comprimento e a carga de um condensador cilíindrico cujo dieléctrico é Poliestireno, a segunda recta é equivalente para um condensador de ar. A razão dos dois declives será igual á constante dielétrica relativa do PVC.
Protocolo Avançado
Determinação da constante dielétrica do ar
Considerando a lei de Gauss, consegue-se determinar a capacidade do condensador cilindrico cuja expressão é dada por
\[ C = \frac{ 2 \pi \epsilon _0 }{ ln(\frac{b}{a}) } L \]
Efetuando uma regressão linear sobre a secção sem dielétrico (ou seja, onde o dielétrico é o ar) consegue-se determinar o valor da capacidade com elevada confiança. Com base neste valor, invertendo a fórmula, determina-se o valor da permitividade do ar (próximo do vazio, ou seja, \( \epsilon _0 \)).
Ligações
- Versão em Inglês (English Version)
- [http://pt.wikipedia.org/wiki/Poliestireno | Página da Wikipédia sobre o Poliestireno